Srinivas Yadav
Introduction
Vectorization is a technique to allow incore parallelism using CPU vector registors which enables us to exploit data-parallelism. Recent additions in C++17 and C++20 to parallel algorithms accept execution policy as first argument which changes the execution behaviour based on the given policy. We implement two new execution policies hpx::execution::simd and hpx::execution::par_simd. The former policy does execution in sequential fashion with Vectorization added, where as the latter one does execution in parallel with Vectorization. For both of these newly implemented policies, the iterator function now no longer accepts static types instead accept only generic types i.e templated or generic function objects. This allows the function object to work with both non-simd and simd policies with a very little or no change in the code. We used std::experimental::simd (_available in C++20 with GCC >= 11.1 and Clang >= 12) as the Vectorization backend in implementing the 2 new execution policies. In the following sections we dicuss example codes on how to use these new facilites adapted to hpx and the benchmarks with results performed on various architectures using different kernels.
Example Usage
The following example code snippet describes the use of hpx for_each algorithm with different execuction policies such as seq, par, simd and par_simd.

Note that we passed a generic lambda to for_each algorithm as argument because the same lambda can be used with different execution policies. The template argument ExPolicy is used to accept execution policy, T is used for handling data-types for creating std::vector and Gen is used to accept geneartor function to fill the std::vector. If the execution policy is seq or par then variable x would be of arithmetic type T as int, float and so on.. where as if execution policy is simd or par_simd then x would of type std::experimental::simd<T> as std::experimental::simd<int>, std::experimental::simd<float> and so on. std::experimental::simd<T> is a vector_pack of type T which is value_type of iterator nums. Contigous elements of the iterator are loaded internally into the vector_pack. The sin and cos functions in the lambda are adapted to arithmetic types and vector_pack types (available in std::experimental namespace).
The lambda used in this code snippet is a compute-bound kernel because of high Arithmetic Intensity due to loop running for 100 steps performing sin and cos operations at each step.
Now, we look into another example using a memory bound kernel (performing SAXPY Operation) with help of transform algorithm.

This code snippet is very similar to the previous with change in lambda and algorithm. Here as well, the arguments to lambda is of two types either arithmetic type (if execution policy is seq or par), or vector_pack type (if the execution policy is simd or par_simd).
The following code snippet describes the usage of algorithms such as count, find. These do not require any lambda and hence vectorization is straightforward just with implementation itself.

This class of algorithms is much easier and are more prone to getting vectorized because of minimum intervention with users i.e no lamda or function is taken in the arguments. Note that we get vectorization benefits only if the iterators passed to algorithm are random access iterators.
Example Implementation
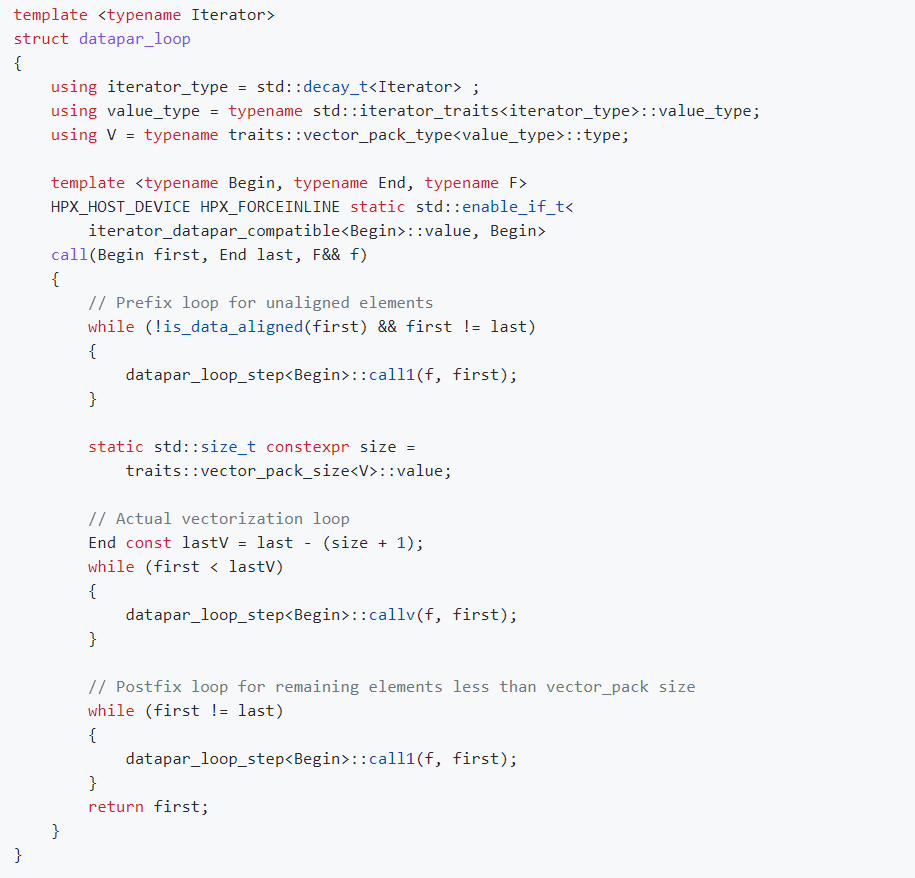
The above code snippet shows implementation for datapar_loop function, which is main vectorization backend helper function for most of the iterative algorithms in hpx. The function call in datapar_loop class can be divided into 3 main steps.
- First a prefix loop runs the code in sequential fashion by calling each element with function f using the helper function datapar_loop_step::call1. This loop runs until it finds first aligned element.
- Secondly, the main vectorization loop, where actual vectorization happens with datapar_loop_step::callv function which actually creates a vector_pack then loads the elements from iterator and calls the function f and then stores back the results as below.

- Finally, the last block i.e post-fix loops handles the elements at the end of array or container that are less than vector_pack size and hence cannot be fit into single vector_pack. So they are handled in sequential fashion similar to pre-fix loop.
Benchmarks
We ran the benchmarks for 2 classes of algorithms. First class being iterative algorithms where each element from the iterator gets mapped using some function. We used for_each and transform algorithms with compute bound and memory bound kernels. For the second class of algorithms, we pick the algorithms which have consists of conditional statements and these can be called as algorithms with simd mask reductions. For this class, we chose count and find algorithms.
Results
The Following figure shows benchmark of for_each algorithm with compute bound kernel i.e Example 1. These benchmarks were run on Intel Xeon Skylake with AVX512. AVX512 vector register can hold 16 floating point elements. We can see a 12x speed up with simd policy and over 140x with par_simd.
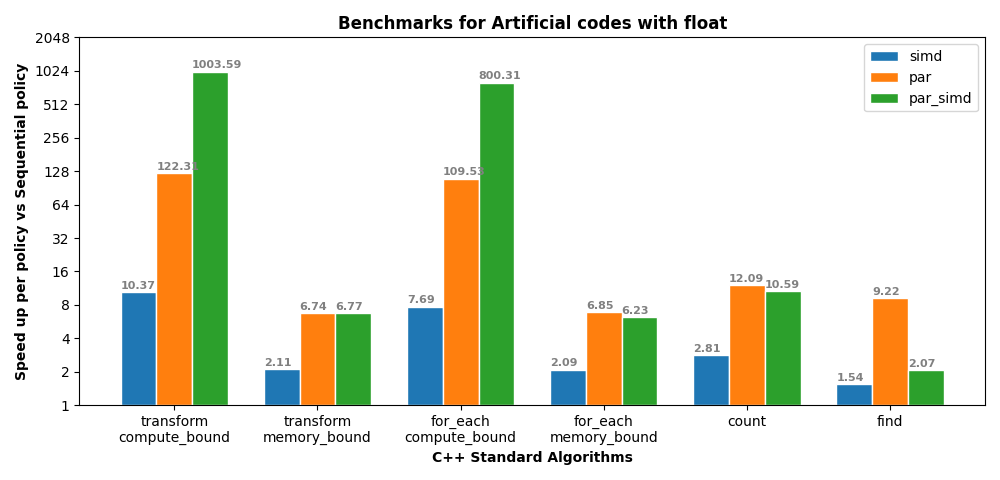
The above image shows the benchmark results graph depeciting speed ups of simd, par and par_simd against seq execution policy. These benchmarks were run on AMD EPYC 7H12 with AVX2. AVX2 vector register can hold 8 floating point elements.The array used contains 128 Billion elements with float and double as data types. We can see super-linear scaling for simd speed up in compute bound kernels i.e speed up of simd (10.37) is more than vector_pack size (8) because sin and cos implementations for scalar arithmetic types and vector_pack types are slightly different. We can see a 3 order magnitude of speed up when using par_simd execution policy.
Conclusion
From the examples illustrated and the benchmarks, we can see how easy it is to vectorize the code using simd and par_simd execution policies and gain massive speed ups with very little change in code. Currently adapting algorithms to simd and par_simd policies is still under progress. You can find the list of algorithms adapted to these policies .
